September 15, 2023
How to optimize your gas consumption without getting REKT, Part 1
Author:
 Netanel Rubin-Blaier
Netanel Rubin-BlaierIn this post (the sequel to “How to optimize your gas consumption without getting REKT”), we focus our attention on Solidity/Yul libraries that realize the mathematical and economic computations that lie at the heart of the DeFi world, and explain why equivalence checking is a potent tool in the hands of developers and auditors who wish to work on such code.
Our plan is:
1. We discuss arithmetic vulnerabilities and the resulting economic exploits against DeFi protocols using the class of Constant Function Market Maker (CFMM) as a motivating example.
2. We examine some recent cases in detail, and explain the PRBMath library rounding error found by Certora.
3. We show how we can both detect the bug using an easy 3-line “equivalence spec” and prove that its correction is bug-free.
Note: Since this is the second part in this series, we will freely use the terms: equivalence checking, formal verification, the Certora Prover, Certora Verification Language (CVL), that were discussed in the previous blog post. You can Readers refresh your memory by reading the first installment here: Part 1.
A crash course in Automated Market Makers (AMM’s)
A distributed finance (or DeFi) application is a rule-based financial system which operates according to protocols implemented by smart contracts on one (or several) blockchains. An important category of DeFi applications is distributed exchanges (or DEX’s). These are defined as a marketplace where users (called traders) can exchange cryptocurrencies in a non-custodial manner (i.e. without the need for an intermediary actor to facilitate the transfer and custody of funds, but possibly with the help of an intermediary smart contract). Unlike traditional (or even centralized crypto) exchanges, which often rely on the order book model or on designated market makers for liquidity provision, most DEX’s rely on a class of protocols known as automated market makers (AMMs).
At the heart of each AMM is a collection of liquidity pools. Each such pool corresponds to a pair of fungible crypto assets (or tokens), which we denoted as token A and token B in the diagram below.
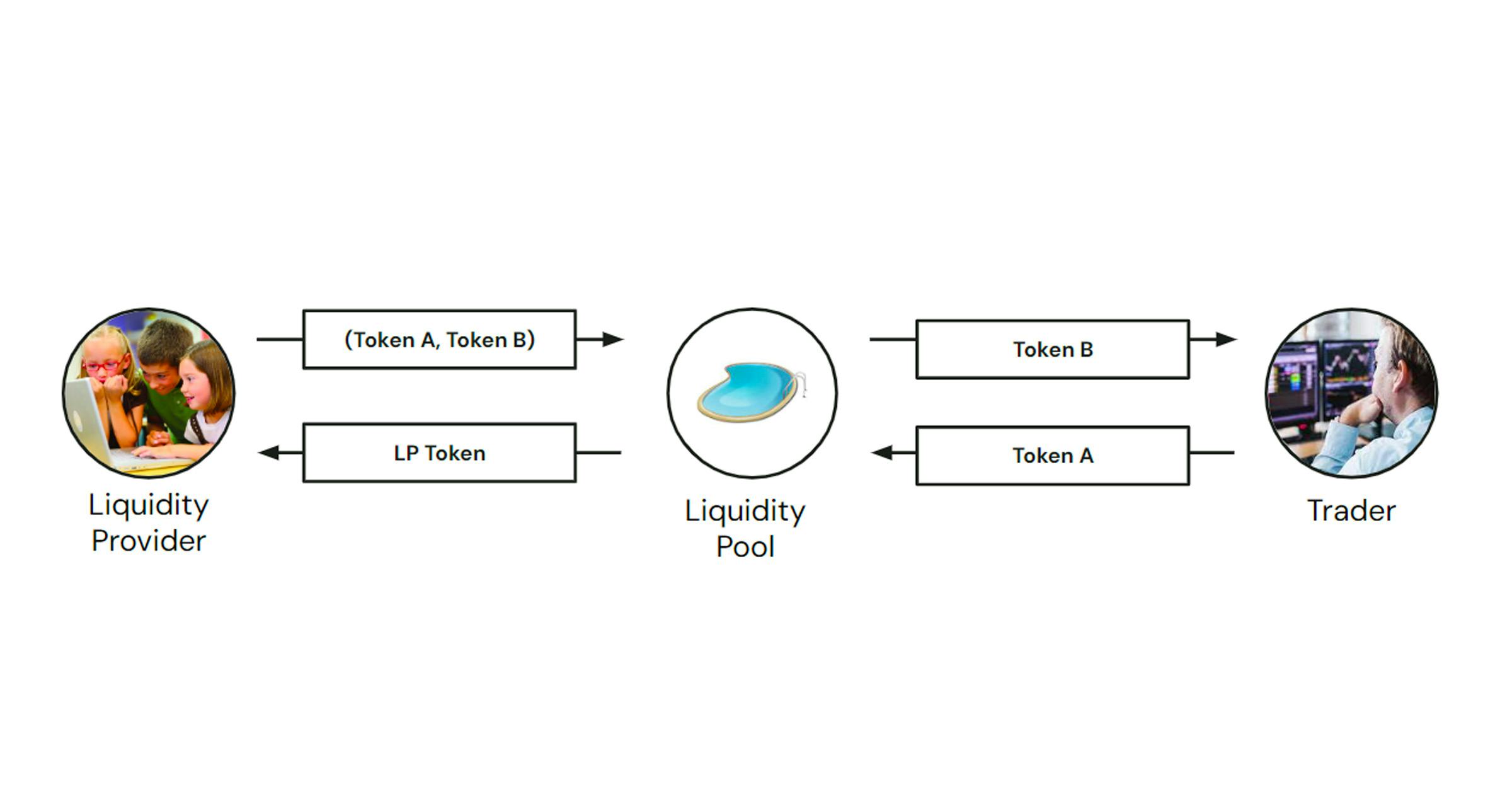
Users who deposit a certain quantity of each token into the pool are called liquidity providers (or LP’s for short). In return for their investment, they receive a liquidity token which essentially functions as a ‘warehouse receipt’, and records the value of their investment relative to the current balance of token A and token B deposited in the pool.
As opposed to order books (a peer-to-peer protocol for matching buyers and sellers), an AMM implements a peer-to-pool method where each user who wishes to trade some amount of token A for token B interacts with the pool itself. In this way, traders have immediate access to liquidity without the need to wait for a counterparty, while LPs profit from investment due to the exchange fees accumulated by the pool.
Constant Function Market Makers (CFMMs) and the trade invariant
As you may have noticed at this point, there is one very important detail that our description above has glossed over.
Question: Suppose that a trader wishes to swap 1000 A-Tokens. How does the AMM know exactly how many B-Tokens to send back?
The key point is that AMM does not require access to an outside source of pricing information (i.e. a pricing oracle) since every market is, in its essence, a price-discovery mechanism.
From a mathematical standpoint, almost every AMM in existence today belongs to a class known as constant function market makers (CFMM’s). That means that its trading (or “swapping”) behavior is governed by a single function
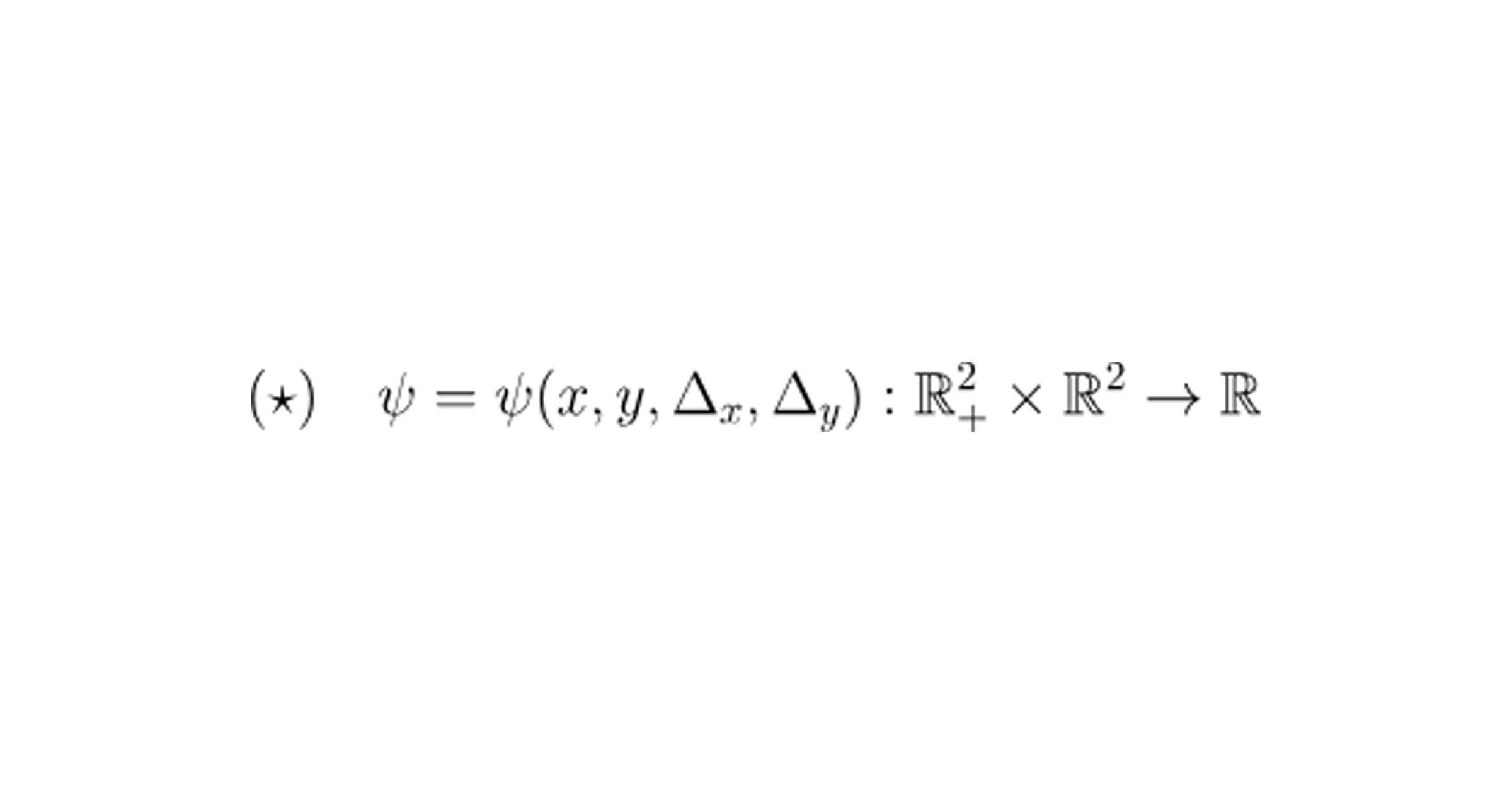
whose inputs are:

The AMM will accept a trade offer if and only if it believes the offer is favorable to it. In concrete terms, this means the AMM should accept a trade if and only if the inequality
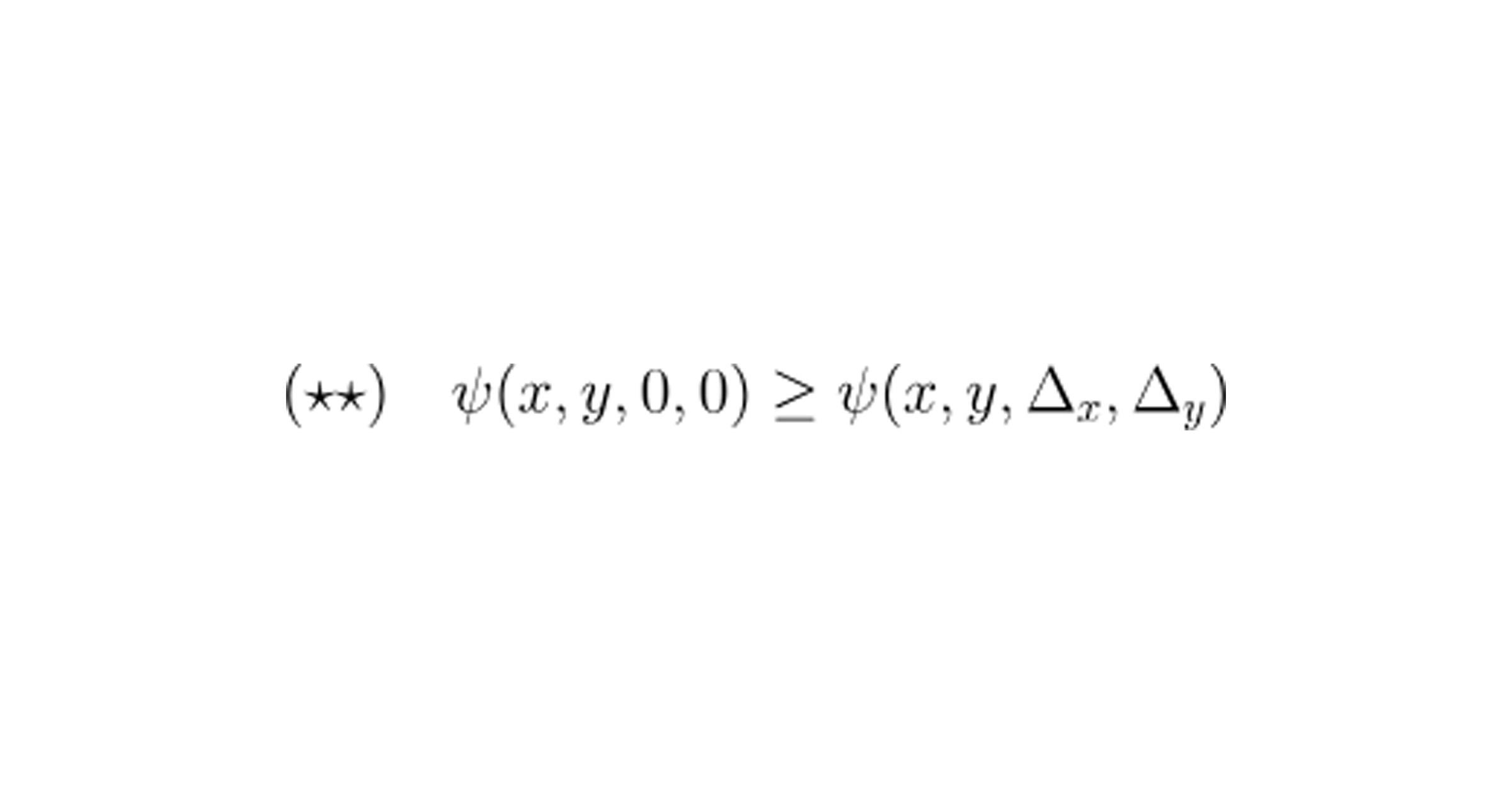
holds.
Example:
The constant product market maker: This is the most classical case, introduced by Martin Koppelmann and Vitalik Buterin in 2018 and first implemented by Uniswap in 2018. This CFMM’s trade function (★) is of the form
Unpacking the formula, we see that if we denote the product of the two reserves by the familiar notation k := x*y, then inequality (★★) precisely states that k must be non-decreasing with each trade, which is a well-known invariant of constant-product AMM’s.
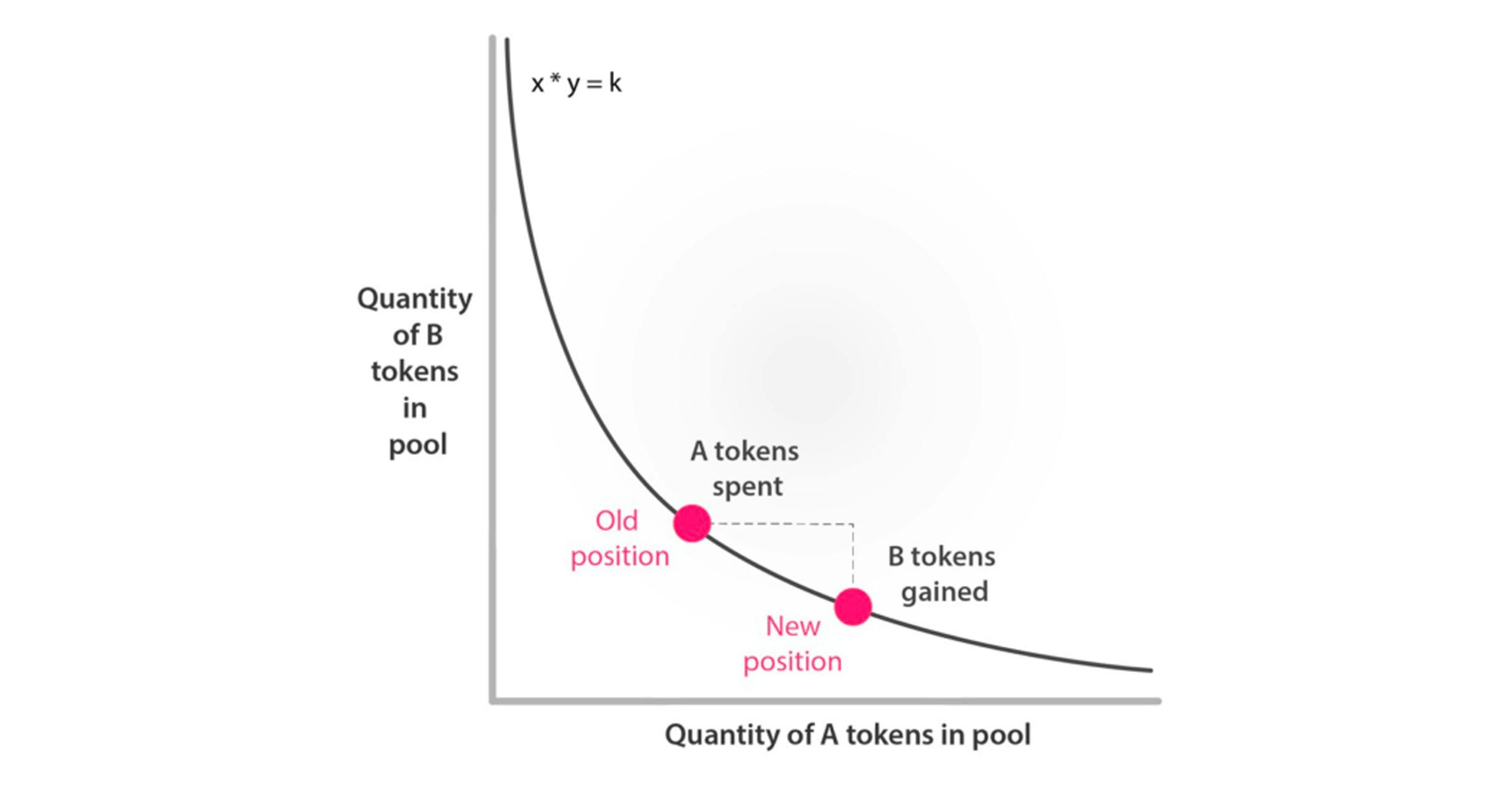
What we would like to emphasize here is that there is nothing magical about the x*y = k formula! There are many other kinds of trade functions, some of them quite mathematically involved.
This should come as no surprise: when the intended use cases are different (e.g. stable coins, derivatives, certain types of synthetic assets), the design of the CFMM invariant should reflect that because different trading functions optimize different properties of the underlying token pairs.
Exploiting the trade function
Question: What would happen if, due to an arithmetic bug or implementation error, it is possible for a user to interact with the AMM’s smart contracts in a way that violates inequality (★★)?
In such a case, it would be possible for an attacker to force the AMM to consistently execute unfavorable trades, thereby draining the funds the liquidity providers (LP’s) have deposited into the pool.
This type of attacking transactions is subtle: the amount of LP-Tokens held by each liquidity provider remains the same before and after each such an attack. However exploiting such a flaw enables an attacker to sip away their worth. A rough but useful analogy to what happens here is inflation: the LP’s are left with the same amount of cash (LP-Tokens) but the same quantity of cash can now buy a lot less goods (A or B-Tokens).

Recent examples of such attacks include:
- The Alpha Homora exploit (Feb 2021)
- The spl-token-lending bug in the Solana Program Library (Dec 2021)
- Yieldly HDL distribution pool exploit (Mar 2022)
- The Hundred Finance exploit (April 2023)
- The Midas Capital exploit (June, 2023)
Perhaps the most common type of such arithmetic bug is an off-by-one error that occurs when one computes the trade function and rounds the result in the wrong direction¹.
Description of the Bug
Remark: As we’ve mentioned in the disclosure, the rounding error we found is present in multiple versions of the PRBMath library. For easy simplification, we will always be referring to commit e2fc29127c (v4.0) throughout this section.
Roughly speaking, the PRBMath library Common.sol function
implements the following algorithm (credit: Remco Bloeman) for efficient computation of unsigned multiplication-and-division:
1. Use the Chinese Remainder Theorem (CRT) to obtain a 512-bit representation of the numerator as an ordered pair (prod1,prod0) of two uint256 variables (for explanation, see Remco’s chinese remainder theorem and full multiplication posts):
2. Make division exact by subtracting the remainder from (prod1,prod0):
3. Calculate the largest power of two divisor (LPOTD) of the denominator and divide by it (see the Remco’s posts and the stackexchange question for an explanation):
4. Invert the denominator mod 2²⁵⁶ using the Newton-Raphson iteration method. (See the post and the paper for the initial guess; Note: This works in a finite field because of Hensel’s lifting lemma):
5. We can now divide by multiplying prod0 with the modular inverse of the denominator:
which produces us the required result.
Knowing that, we can now review the computation of signed multiplication-and-division is realized by the Common.sol function:
which builds upon the aforementioned computation by implementing the following algorithm:
- Extract the absolute value of the inputs:
2. Compute the absolute value of the result by reducing to the unsigned case (i.e. invoking the previously mentioned unsigned multiplication-and-division function on the absolute values of the inputs):
3. Revert with a custom error if the absolute value of the result cannot fit in a int256-variable:
4. Efficiently compute the sign of each input:
5. Compute the overall sign by taking XOR and return the result:
The problem is that Step 2 in the algorithm of mulDivSigned is wrong since
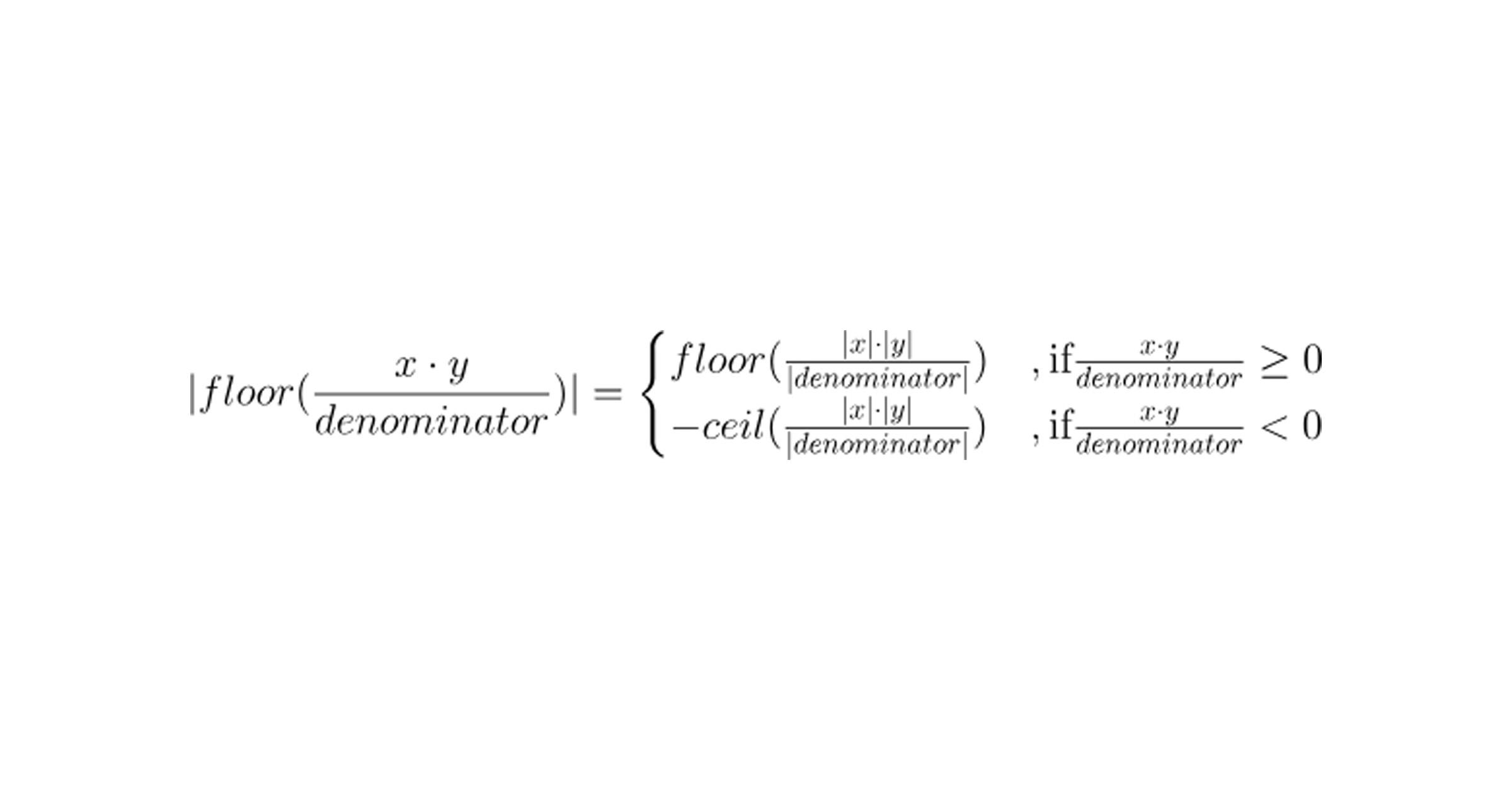
Thus, whenever the result is negative, we are actually rounding towards zero and not minus infinity, leading to an off-by-one error.
Example: Take
then:
and therefore:
but:
Equivalence Checking and Easy Specs
In general, writing formal specifications is hard work. However, for computational libraries the required behavior is easy to describe mathematically that the spec almost writes itself. Consider the two PRBMath functions we discussed in the previous section.
Looking only at the NatSpec comments for the function, we can produce a spec for mulDivSigned:
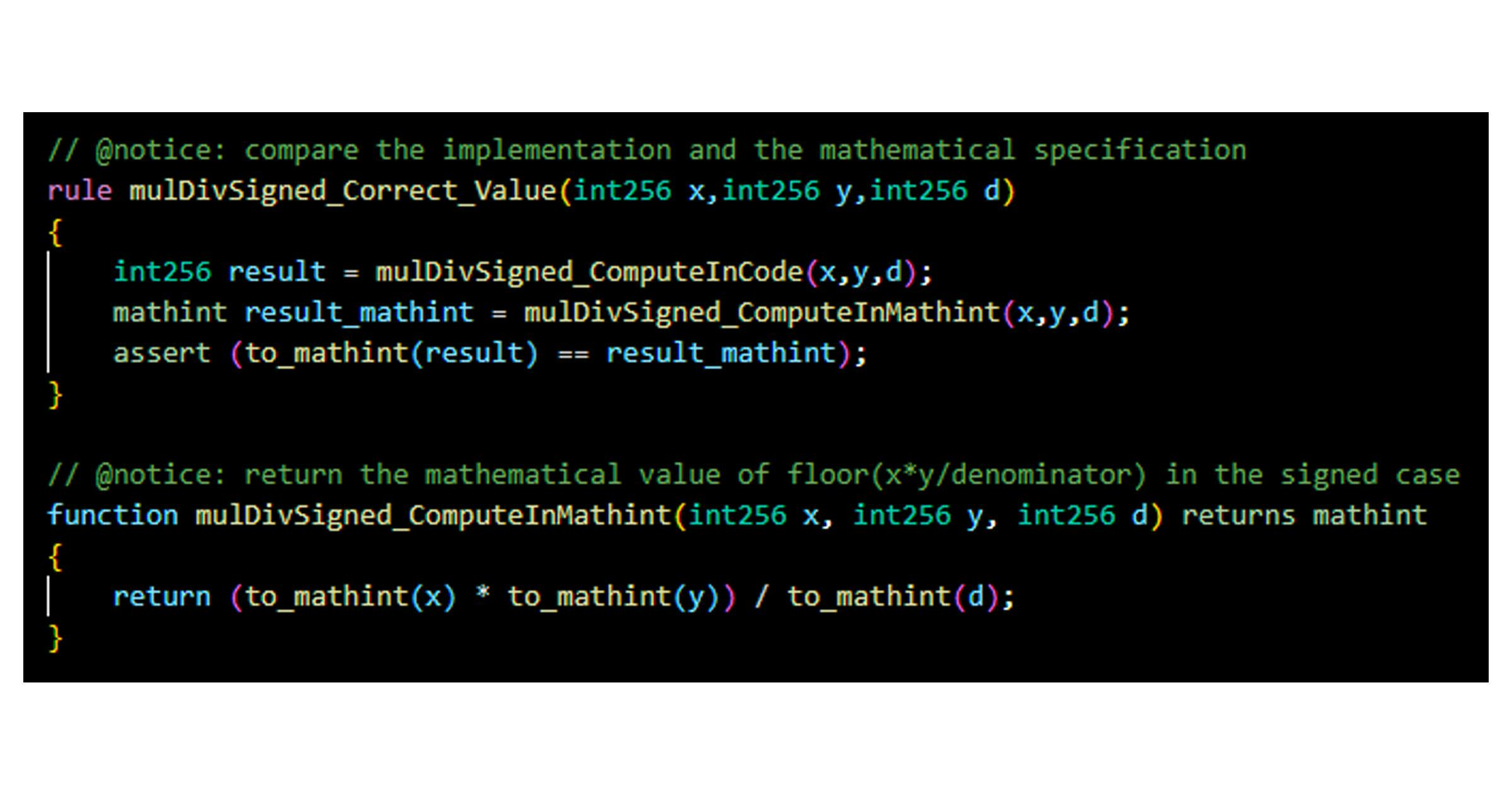
Running this spec² via the Certora Prover produces the counterexample which shows that mulDivSigned has an off-by-one error:
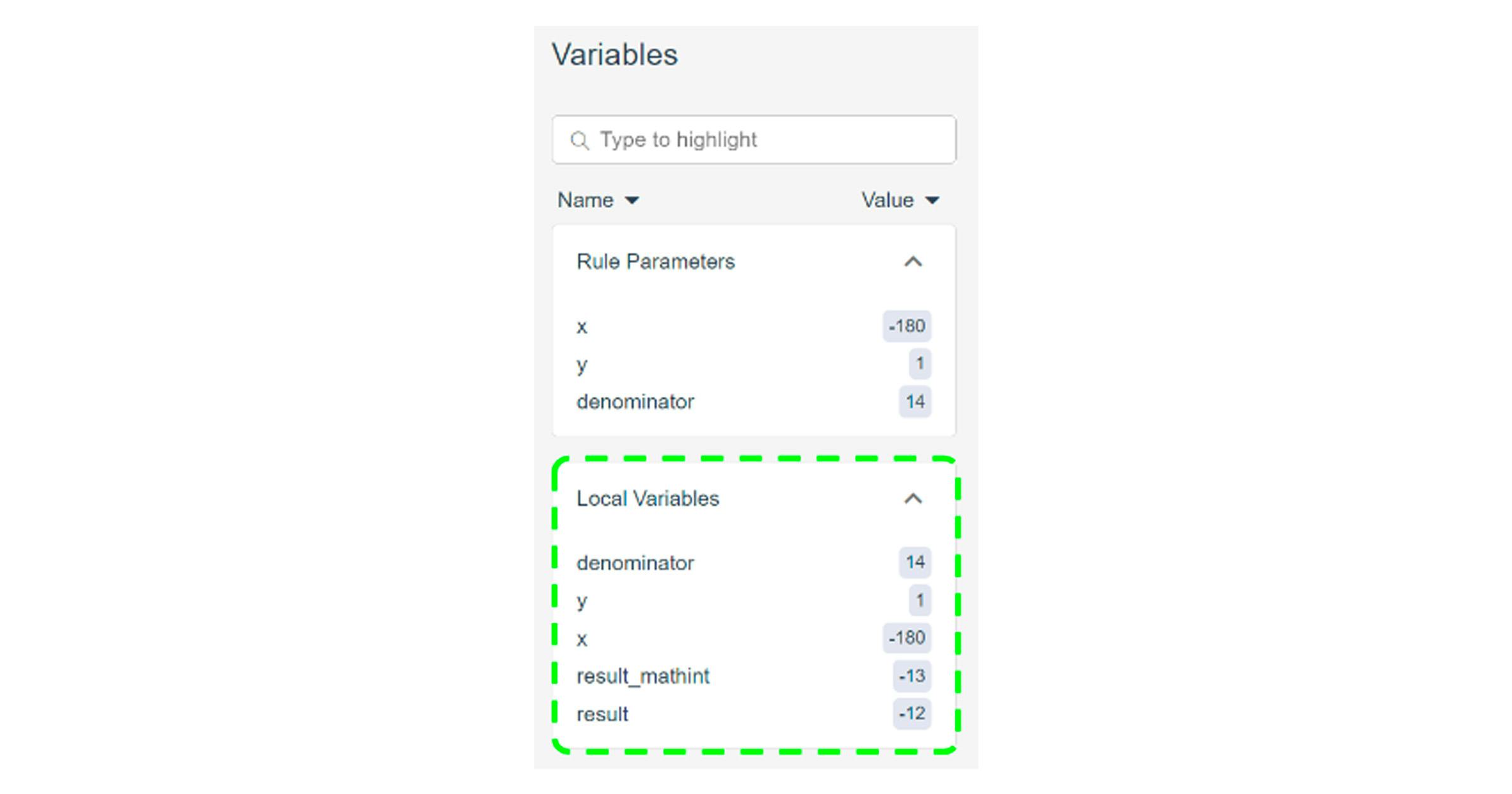
and that’s it! That’s the whole secret. We didn’t even need to read the code or understand how mulDivSigned (or mulDiv) is implemented.

Conclusion
Mathematical libraries are the basic building blocks of the DeFi ecosystem. However, they are surprisingly hard to get right (especially when one tries to aggressively optimize their gas consumption), and auditing them can be tiresome and difficult.
The bug above demonstrates the importance of Certora’s equivalence checker and the expressibility of the CVL Language: an elementary CVL spec (an “equivalence spec”) can detect bugs in the Solidity code of a mathematical library which involves extensive Yul segments, numerous bit-hacking tricks, and even a bit of number theory thrown into the mix —
all without the need to even understand anything about the details of the implementation!
¹ Even though all of our discussion so far was in the context of AMM-based DEX’s, we should at least mention that this problem occurs in other DeFi applications as well. For example, in the case of lending and borrowing platforms, it is already noted in ERC-4626 (under “security considerations”) that “… Vault implementers should be aware of the need for specific, opposing rounding directions across the view methods… ”. However, for the sake of simplification , we have chosen to focus on one class of DeFi applications instead of trying to categorize this type of vulnerability in full generality.
² In the terminology used in part 1, producing this spec is the “second mode” of the equivalence checker, which compares Solidity or Yul code against logical expressions written in Certora Verification Language (CVL). To be precise, we are only producing half of the equivalence spec here since we need not concern ourselves with the revert conditions.
 Uri Kirstein
Uri Kirstein Yura Sherman
Yura Sherman